Diffie-Hellman par Admin
posté par Admin le 5/2/2018
En cryptographie, l'échange de clés Diffie-Hellman, créé par Whitfield Diffie et Martin Hellman, est une méthode qui permet à deux agents d'échanger une clé après avoir choisi un nombre secret, sans qu'une tierce personne puisse savoir le secret, même en ayant écouté tous leurs échanges.
Cette méthode, publiée en 1976, a changé l'histoire de la cryptographie et a été la base de la cryptographie asymétrique ce qui a rendu possible la communication sécurisée sur internet.
“We've heard a good bit in this courtroom about public key encryption," said Albright. "Are you familiar with that?" "Yes, I am," said Diffie, in what surely qualified as the biggest understatement of the trial. "And how is it that you're familiar with public key encryption?" "I invented it.”
Avant la création du protocole d'échange de clés diffie-hellman, les clés de cryptage devaient être physiquement transmises à l'autre agent à qui nous voulions parler. Ce protocole éliminait l'un des plus grands défauts du cryptage symétrique: l'échange de clés. L'échange pourrait maintenant se faire secrètement et en toute sécurité. Ce nouveau protocole a changé le monde de la cryptographie en étant la base du chiffrement asymétrique.
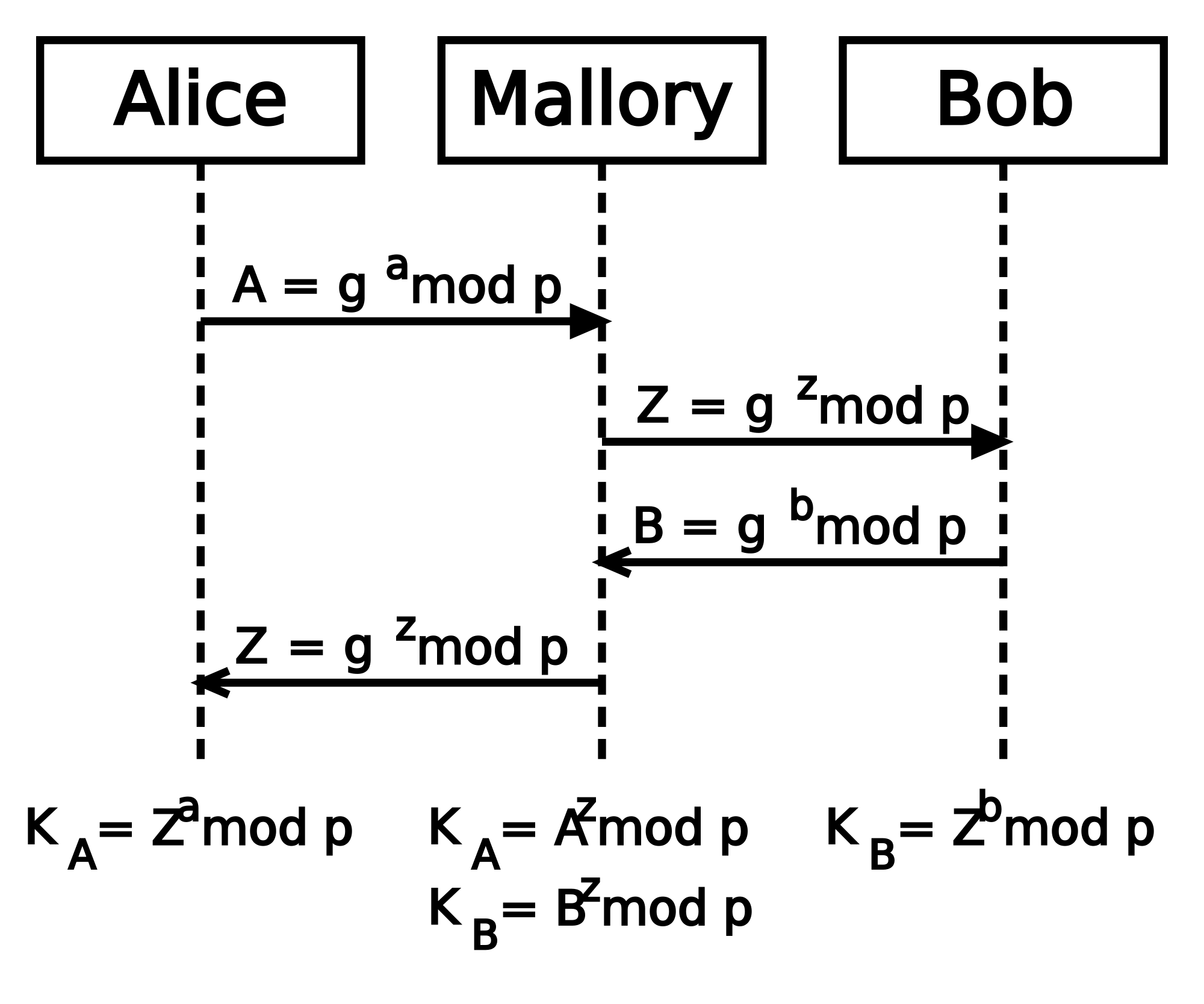
Principe de fonctionnement:
- Alice choisit deux nombres premiers p et g publics, que tout le monde peut lire.
- Alice choisit un nombre secret a
- Elle envoie à Bob la valeur A = ga mod p
- Après avoir reçu la valeur A, Bob à son tour choisit un nombre secret b
- Bob envoie à Alice la valeur B = gb mod p
- Alice peut maintenant calculer la clé secrète : Ba mod p
- Bob fait de même et obtient la même clé qu'Alice : Ab mod p
Cette méthode fonctionne grace à un simple calcul:
(ga mod p)b mod p = g(ab) mod p
(gb mod p)a mod p = g(ba) mod p
Pas un grand fan de maths?
Ce protocole d'échange de clés est assez simple, mais, les choses
peuvent sembler un peu compliquées avec trop de maths, alors voici une
simple analogie de peinture expliquant le protocole.
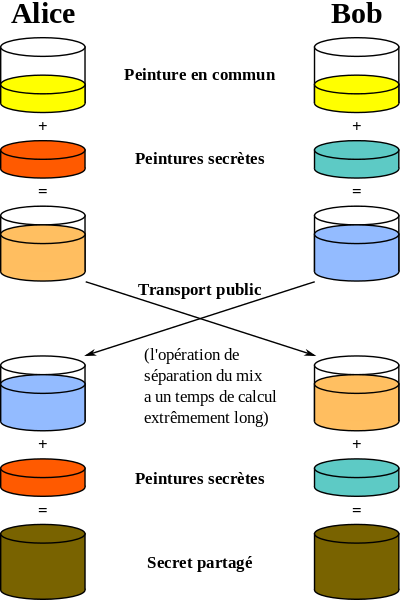
Pour rendre les choses complètement claires, voici un simple code python qui représente le protocole d'échange de clés diffie-hellman:
from __future__ import print_function # Variables p = 23 g = 5 ##choisire valeurs pour p et g, or p et g sont des nombres premiers a = 6 b = 15 # ce code va imprimer le debut, les variables avant le calcul print( "Variables publiques:") print( " p: " , p ) print( " g: " , g ) # Alice envoie a bob A = g^a mod p A = (g**a) % p print( "\n A: ", A ) # Bob a Alice B = g^b mod p B = (g ** b) % p print( "\n B: ", B ) print( "\n------------\n" ) print( "le secret prive:" ) # Alice calcul le secret: s = B^a mod p As = (B ** a) % p print( " secret d'Alice: ", As ) # Bob calcul le secret: s = A^b mod p s = (A**b) % p print( " secret de Bob: ", s )
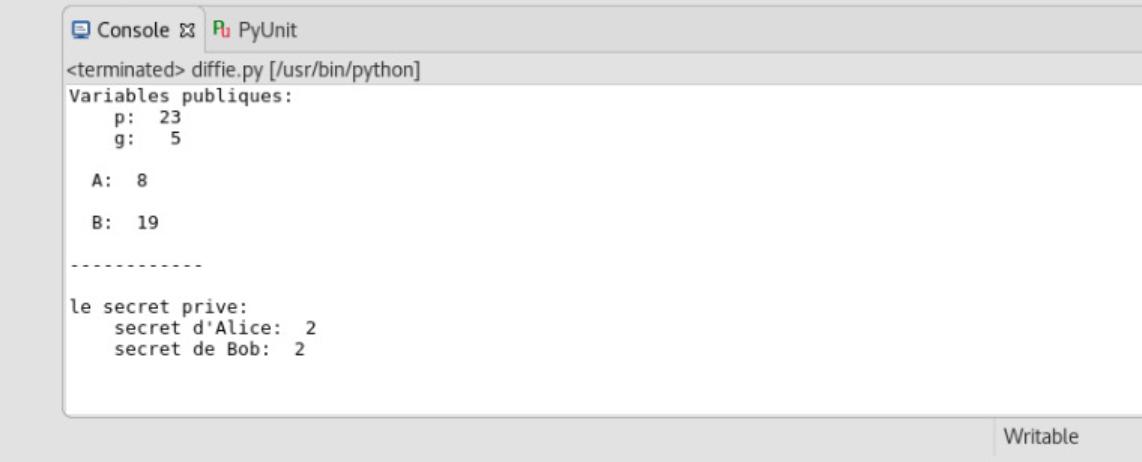
Sortie de la console après avoir exécuté le code ci-dessus.